Solution minimale du jeu Traffic!

Un article de Wikipedia.

(Différences entre les versions)
(→Solutions de grilles)
(→Solutions de grilles)
Ligne 129 : Ligne 129 :
| 39 || [[Image:Traffic39.jpg]] || 12 || || 50 || 00:59:53 || 3581
| 39 || [[Image:Traffic39.jpg]] || 12 || || 50 || 00:59:53 || 3581
|- align="center"
|- align="center"
-
| 40 || [[Image:Traffic40.jpg]] || 13 || || 51 || 00:52:22 || 3024
+
| 40 || [[Image:Traffic40.jpg]] || 13 ||
 +
# (4,1)->(5,1)
 +
# (4,2)->(4,1)
 +
# (6,3)->(6,4)
 +
# (1,3)->(4,3)
 +
# (3,1)->(3,2)
 +
# (1,1)->(2,1)
 +
# (1,4)->(1,1)
 +
# (2,4)->(2,2)
 +
# (2,6)->(1,6)
 +
# (3,4)->(3,5)
 +
# (4,4)->(1,4)
 +
# (3,5)->(3,4)
 +
# (5,5)->(5,4)
 +
# (1,6)->(4,6)
 +
# (3,4)->(3,5)
 +
# (1,4)->(3,4)
 +
# (1,1)->(1,4)
 +
# (2,1)->(1,1)
 +
# (3,2)->(3,1)
 +
# (2,2)->(2,5)
 +
# (4,3)->(1,3)
 +
# (6,4)->(6,3)
 +
# (4,6)->(5,6)
 +
# (3,4)->(2,4)
 +
# (4,1)->(4,5)
 +
# (5,1)->(4,1)
 +
# (5,2)->(4,2)
 +
# (1,3)->(3,3)
 +
# (2,4)->(3,4)
 +
# (2,5)->(2,2)
 +
# (3,4)->(2,4)
 +
# (4,5)->(4,4)
 +
# (5,6)->(4,6)
 +
# (6,3)->(6,4)
 +
# (3,3)->(4,3)
 +
# (3,1)->(3,2)
 +
# (1,1)->(2,1)
 +
# (1,4)->(1,1)
 +
# (2,4)->(1,4)
 +
# (3,5)->(3,4)
 +
# (4,6)->(1,6)
 +
# (4,4)->(4,5)
 +
# (3,4)->(3,5)
 +
# (5,4)->(5,5)
 +
# (1,4)->(2,4)
 +
# (1,1)->(1,2)
 +
# (2,1)->(1,1)
 +
# (3,2)->(3,1)
 +
# (4,3)->(3,3)
 +
# (6,4)->(6,1)
 +
# (2,4)->(5,4)
 +
|| 51 || 00:52:22 || 3024
|}
|}

Version du 22 avril 2008 à 11:00

Sommaire

Solution minimale du jeu Traffic!

But

Déterminer le nombre minimal de mouvements pour résoudre une grille du jeu Traffic!.

Introduction

Premièrement, Merci à Phillip Cheng pour l'implémentation de Traffic! et un Grand Merci posthume à Nob Yoshigahara pour sa lumineuse idée.


Traffic! est une implémentation gratuite sous Palm du jeu 'Rush Hour' conçu par Nob Yoshigahara.

Il consiste en un plateau carré de 6 unités sur lequel se trouve des blocs de 2 ou 3 unités qui peuvent se déplacer verticalement ou horizontalement.

Le but du jeu est de faire sortir un bloc de 2 unités horizontalement en déplaçant les autres blocs.

Une croquis vaut mieux qu'un long discours, donc voici une image d'une grille de Traffic! :

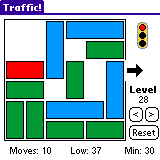
Image:Traffic.gif

Le bloc blanc doit être déplacé vers la sortie.

Résultats

La méthode utilisée pour résoudre une grille de Traffic! est de disposer de trois listes.

  • La première contient la liste des grilles en traitement.
  • La deuxième contient la liste des grilles à traiter à la prochaine étape.
  • La troisième contient la liste des grilles déjà connues.

Méthode de résolution d'une grille

Initialement (niveau 0), la première et la troisième liste contiennent la liste de Traffic! à résoudre; la deuxième liste est vide.

A chaque niveau de la résolution,

  • Pour chaque grille de la première liste, l'ensemble des coups (déplacements des blocs) est calculé.
  • S'il est possible de terminer une grille par le déplacement du bloc à sortir de la grille, c'est le seul coup qui est considéré pour la grille.
  • Si jouer le coup pour la grille en question conduit à une grille inconnue, c'est à dire qui n'est pas dans la troisième liste, cette nouvelle grille est ajoutée à la deuxième liste et à la troisième liste des grilles connues.
  • Sinon un nouveau coup est considéré, jusqu'à épuisement des coups et des grilles de la première liste.
  • A la fin du niveau, la deuxième liste des grilles à traiter prend la place de la première liste des grilles en traitement et la deuxième liste redevient vide.

Solutions de grilles

Niveau Grille Nombre de blocs Solution Nombre de coups Durée des calculs (HH:MM:SS) Nombre de grilles différentes
1 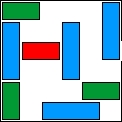Image:Traffic1.jpg 8 Media:Anim1.swf
  1. (5,2)->(2,2)
  2. (6,4)->(6,1)
  3. (1,6)->(2,6)
  4. (1,3)->(1,4)
  5. (1,1)->(1,2)
  6. (3,1)->(1,1)
  7. (4,3)->(4,1)
  8. (2,4)->(5,4)
8 00:05:41 1067
2 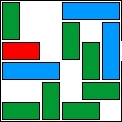Image:Traffic2.jpg 11 8 00:29:01 2753
3 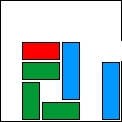Image:Traffic3.jpg 6 14 00:01:40 770
4 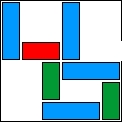Image:Traffic4.jpg 7 9 00:00:23 356
5 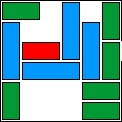Image:Traffic5.jpg 11 9 00:23:14 2139
6 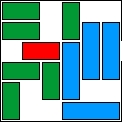Image:Traffic6.jpg 11 9 00:14:30 1637
7 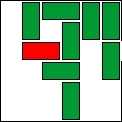Image:Traffic7.jpg 9 13 01:23:17 4613
8 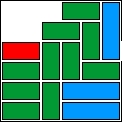Image:Traffic8.jpg 14 12 00:05:05 950
9 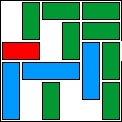Image:Traffic9.jpg 12 12 00:01:47 681
10 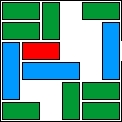Image:Traffic10.jpg 12 17 00:16:32 1847
11 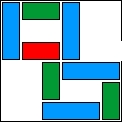Image:Traffic11.jpg 8 25
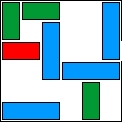12 Image:Traffic12.jpg 8 17 00:04:45 1267
13 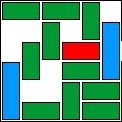Image:Traffic13.jpg 13 16
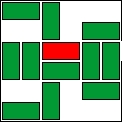14 Image:Traffic14.jpg 12 17
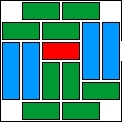15 Image:Traffic15.jpg 14 23
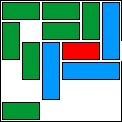16 Image:Traffic16.jpg 11 21
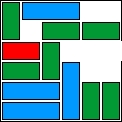17 Image:Traffic17.jpg 12 24
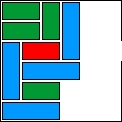18 Image:Traffic18.jpg 9 25
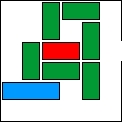19 Image:Traffic19.jpg 8 22
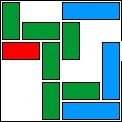20 Image:Traffic20.jpg 9 10
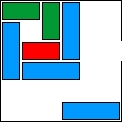21 Image:Traffic21.jpg 7 21
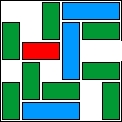22 Image:Traffic22.jpg 12 26
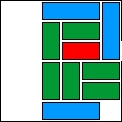23 Image:Traffic23.jpg 10 29
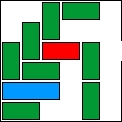24 Image:Traffic24.jpg 10 25
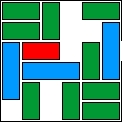25 Image:Traffic25.jpg 13 27
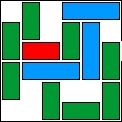26 Image:Traffic26.jpg 12 28
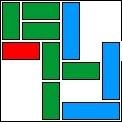27 Image:Traffic27.jpg 10 28
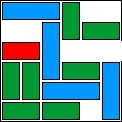28 Image:Traffic28.jpg 12 30
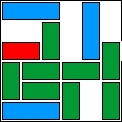29 Image:Traffic29.jpg 12 31
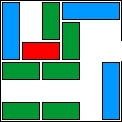30 Image:Traffic30.jpg 10 32 00:05:39 1158
31 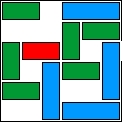Image:Traffic31.jpg 11 37 01:18:17 3947
32 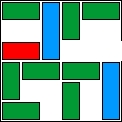Image:Traffic32.jpg 11 37 00:01:09 568
33 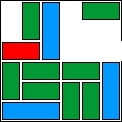Image:Traffic33.jpg 12 40 01:36:05 3960
34 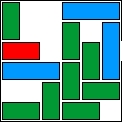Image:Traffic34.jpg 12 43 01:58:33 4364
35 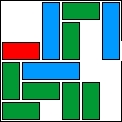Image:Traffic35.jpg 11 43
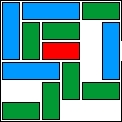36 Image:Traffic36.jpg 12 44 00:33:37 2556
37 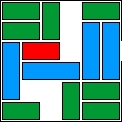Image:Traffic37.jpg 13 47 00:24:18 1941
38 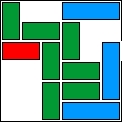Image:Traffic38.jpg 11 48 01:01:16 3755
39 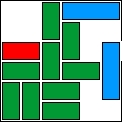Image:Traffic39.jpg 12 50 00:59:53 3581
40 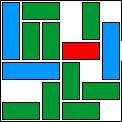Image:Traffic40.jpg 13
  1. (4,1)->(5,1)
  2. (4,2)->(4,1)
  3. (6,3)->(6,4)
  4. (1,3)->(4,3)
  5. (3,1)->(3,2)
  6. (1,1)->(2,1)
  7. (1,4)->(1,1)
  8. (2,4)->(2,2)
  9. (2,6)->(1,6)
  10. (3,4)->(3,5)
  11. (4,4)->(1,4)
  12. (3,5)->(3,4)
  13. (5,5)->(5,4)
  14. (1,6)->(4,6)
  15. (3,4)->(3,5)
  16. (1,4)->(3,4)
  17. (1,1)->(1,4)
  18. (2,1)->(1,1)
  19. (3,2)->(3,1)
  20. (2,2)->(2,5)
  21. (4,3)->(1,3)
  22. (6,4)->(6,3)
  23. (4,6)->(5,6)
  24. (3,4)->(2,4)
  25. (4,1)->(4,5)
  26. (5,1)->(4,1)
  27. (5,2)->(4,2)
  28. (1,3)->(3,3)
  29. (2,4)->(3,4)
  30. (2,5)->(2,2)
  31. (3,4)->(2,4)
  32. (4,5)->(4,4)
  33. (5,6)->(4,6)
  34. (6,3)->(6,4)
  35. (3,3)->(4,3)
  36. (3,1)->(3,2)
  37. (1,1)->(2,1)
  38. (1,4)->(1,1)
  39. (2,4)->(1,4)
  40. (3,5)->(3,4)
  41. (4,6)->(1,6)
  42. (4,4)->(4,5)
  43. (3,4)->(3,5)
  44. (5,4)->(5,5)
  45. (1,4)->(2,4)
  46. (1,1)->(1,2)
  47. (2,1)->(1,1)
  48. (3,2)->(3,1)
  49. (4,3)->(3,3)
  50. (6,4)->(6,1)
  51. (2,4)->(5,4)
51 00:52:22 3024

Conclusions

  • Le nombre minimal des mouvements nécessaires pour résoudre une grille déterminé par ce logiciel correspond à celui indiqué par le programme Traffic!.
  • Dans le programme Traffic! le nombre minimal de mouvements nécessaire à résoudre une grille s'affiche qu'une fois la grille résolue. Une question se pose : Est-ce que le nombre minimal de mouvements pour résoudre la grille est calculé lors de la résolution de la grille ou est-il préalablement connu ?
  • PP Compiler génère une erreur de compilation "Out of memory(1)" si le nombre de grilles spécifiées dans Trafficsamples.pas dépasse les 35. Il faut donc procéder en plusieurs étapes pour résoudre les 40 grilles de Traffic!
  • Un affichage graphique de la grille et de sa solution serait avantageux.

Ressources

Récupérée de « http://zigloo.ch/index.php/Solution_minimale_du_jeu_Traffic%21 »