Graphes et premier nombre de Ramsey
Un article de Wikipedia.
(→''n = 5'') |
(→Statistiques) |
||
| (49 révisions intermédiaires masquées) | |||
| Ligne 30 : | Ligne 30 : | ||
| 6 || 6 || entre ''102'' et ''165'' | | 6 || 6 || entre ''102'' et ''165'' | ||
|} | |} | ||
| + | |||
| + | ==== Anecdote sur les nombres de Ramsey ==== | ||
| + | Paul Erdos disait : "Imaginez une force extraterrestre, vigoureuse et plus puissante que nous qui atterrit et demande la valeur de ''R(5, 5)'' où sinon ils détruiront notre planète. Dans ce cas, nous devrions regrouper l'ensemble des ordinateurs et tous nos mathématiciens pour trouver la valeur. Mais supposons, par contre, qu'ils demandent la valeur ''R(6, 6)'', nous devrions alors tenter de détruire les extraterrestres." (voir [[Graphes et premier nombre de Ramsey#Ressources|Ressources 'The Ramsey Number R(3,3)']]) | ||
=== Permutations === | === Permutations === | ||
| Ligne 178 : | Ligne 181 : | ||
|} | |} | ||
| - | === | + | === Cliques === |
| - | + | Un graphe dont tous les sommets sont reliés entre eux s'appelle une clique. | |
| + | |||
| + | La détermination de la clique maximale d'un graphe s'inspire de l'algorithme décrit dans les ressources ([[Graphes et premier nombre de Ramsey#Ressources|Using Constraint Programming to Solve the Maximum Clique Problem]]). | ||
| + | |||
| + | Le principe de l'algorithme se base sur le fait que dans une clique d'ordre ''n'', si un sommet et ses arrêtes qui le reliait aux autres sont supprimés, alors le graphe est une clique d'ordre ''n - 1''. | ||
| + | |||
| + | La fonction ''omega'' implémente cette détermination, associée à la fonction ''gamma'' qui détermine les nœuds associés à un sommet et la fonction ''limitlinks'' qui supprime un sommet et les arrêtes associées. | ||
== Résultats == | == Résultats == | ||
| - | === ''n = 2'' === | + | === Statistiques === |
| - | {| border="1" cellpadding="10 | + | {| border="1" align="center" cellpadding="5" |
| + | |+ '''Statistiques''' | ||
| + | ! Nœuds !! Arrêtes !! Graphes !! Permutations !! Graphes réduits !! Durée des calculs en secondes | ||
| + | |- align="right" | ||
| + | | 2 || 1 || 2 || 2 || 2 || 0 | ||
| + | |- align="right" | ||
| + | | 3 || 3 || 8 || 6 || 4 || 0 | ||
| + | |- align="right" | ||
| + | | 4 || 6 || 64 || 24 || 11 || 0 | ||
| + | |- align="right" | ||
| + | | 5 || 10 || 1024 || 120 || 34 || 1 | ||
| + | |- align="right" | ||
| + | | 6 || 15 || 32768 || 720 || 156 || 229 | ||
| + | |} | ||
| + | |||
| + | * Nœuds : ''n'' | ||
| + | * Arrêtes : ''n x (n - 1) / 2'' | ||
| + | * Graphes : ''2 ^ (n x (n - 1) / 2) | ||
| + | * Permutations : ''n!'' | ||
| + | * Graphes réduits : graphes équivalents sous les permutations | ||
| + | |||
| + | === Graphes réduits pour ''n = 2'' === | ||
| + | {| align="center" | ||
| + | |- | ||
| + | | | ||
| + | {| border="1" cellpadding="10" | ||
! Nombre d'arrêtes !! Arretes | ! Nombre d'arrêtes !! Arretes | ||
|- | |- | ||
| 0 || | | 0 || | ||
| + | # [] | ||
|- | |- | ||
| 1 || par complément de 0 | | 1 || par complément de 0 | ||
| + | |} | ||
| + | || | ||
| + | [[Image:Graphes2.jpg|thumb|200px|Graphes réduits pour n=2]] | ||
|} | |} | ||
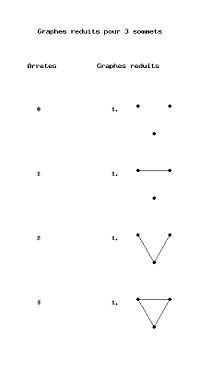
| - | === ''n = 3'' === | + | === Graphes réduits pour ''n = 3'' === |
| - | {| border="1" cellpadding="10 | + | {| align="center" |
| + | |- | ||
| + | | | ||
| + | {| border="1" cellpadding="10" | ||
! Nombre d'arrêtes !! Arretes | ! Nombre d'arrêtes !! Arretes | ||
|- | |- | ||
| 0 || | | 0 || | ||
| + | # [] | ||
|- | |- | ||
| - | | 1 || [(1,2)] | + | | 1 || |
| + | # [(1,2)] | ||
|- | |- | ||
| 2 || par complément de 1 | | 2 || par complément de 1 | ||
|- | |- | ||
| 3 || par complément de 0 | | 3 || par complément de 0 | ||
| + | |} | ||
| + | || | ||
| + | [[Image:Graphes3.jpg|thumb|200px|Graphes réduits pour n=3]] | ||
|} | |} | ||
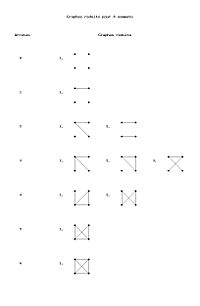
| - | === ''n = 4'' === | + | === Graphes réduits pour ''n = 4'' === |
| - | {| border="1" cellpadding="10 | + | {| align="center" |
| + | |- | ||
| + | | | ||
| + | {| border="1" cellpadding="10" | ||
! Nombre d'arrêtes !! Arretes | ! Nombre d'arrêtes !! Arretes | ||
|- | |- | ||
| 0 || | | 0 || | ||
| + | # [] | ||
|- | |- | ||
| - | | 1 || [(1,2)] | + | | 1 || |
| + | # [(1,2)] | ||
|- | |- | ||
| - | + | | 2 || | |
| + | # [(1,2),(1,3)] | ||
| + | # [(1,2),(3,4)] | ||
|- | |- | ||
| - | | | + | | 3 || |
| - | | | + | # [(1,2),(1,3),(1,4)] |
| - | + | # [(1,2),(1,3),(2,3)] | |
| - | + | # [(1,2),(1,3),(2,4)] | |
| - | + | ||
| - | + | ||
| - | + | ||
|- | |- | ||
| 4 || par complément de 2 | | 4 || par complément de 2 | ||
| Ligne 227 : | Ligne 277 : | ||
|- | |- | ||
| 6 || par complément de 0 | | 6 || par complément de 0 | ||
| + | |} | ||
| + | || | ||
| + | [[Image:Graphes4.jpg|thumb|200px|Graphes réduits pour n=4]] | ||
|} | |} | ||
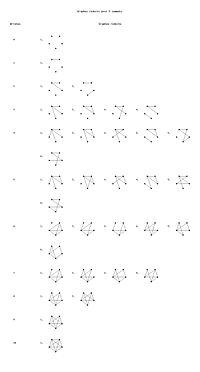
| - | === ''n = 5'' === | + | === Graphes réduits pour ''n = 5'' === |
| - | {| border="1" cellpadding="10 | + | {| align="center" |
| + | |- | ||
| + | | | ||
| + | {| border="1" cellpadding="10" | ||
! Nombre d'arrêtes !! Arretes | ! Nombre d'arrêtes !! Arretes | ||
|- | |- | ||
| 0 || | | 0 || | ||
| + | # [] | ||
|- | |- | ||
| - | | 1 || [(1,2)] | + | | 1 || |
| + | # [(1,2)] | ||
|- | |- | ||
| - | + | | 2 || | |
| + | # [(1,2),(1,3)] | ||
| + | # [(1,2),(3,4)] | ||
|- | |- | ||
| - | |[(1,2),(3,4)] | + | | 3 || |
| + | # [(1,2),(1,3),(1,4)] | ||
| + | # [(1,2),(1,3),(2,3)] | ||
| + | # [(1,2),(1,3),(2,4)] | ||
| + | # [(1,2),(1,3),(4,5)] | ||
|- | |- | ||
| - | | | + | | 4 || |
| + | # [(1,2),(1,3),(1,4),(1,5)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3)] | ||
| + | # [(1,2),(1,3),(1,4),(2,5)] | ||
| + | # [(1,2),(1,3),(2,3),(4,5)] | ||
| + | # [(1,2),(1,3),(2,4),(3,4)] | ||
| + | # [(1,2),(1,3),(2,4),(3,5)] | ||
|- | |- | ||
| - | |[(1,2),(1,3),(2,3)] | + | | 5 || |
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,4)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,5)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(4,5)] | ||
| + | # [(1,2),(1,3),(1,4),(2,5),(3,5)] | ||
| + | # [(1,2),(1,3),(2,4),(3,5),(4,5)] | ||
|- | |- | ||
| - | | | + | | 6 || par complément de 4 |
|- | |- | ||
| - | | | + | | 7 || par complément de 3 |
|- | |- | ||
| - | | | + | | 8 || par complément de 2 |
|- | |- | ||
| - | | | + | | 9 || par complément de 1 |
|- | |- | ||
| - | |[ | + | | 10 || par complément de 0 |
| + | |} | ||
| + | || | ||
| + | [[Image:Graphes5.jpg|thumb|200px|Graphes réduits pour n=5]] | ||
| + | |} | ||
| + | |||
| + | === Graphes réduits pour ''n = 6'' === | ||
| + | {| align="center" | ||
|- | |- | ||
| - | | | + | | |
| + | {| border="1" cellpadding="10" | ||
| + | ! Nombre d'arrêtes !! Arretes | ||
|- | |- | ||
| - | |[ | + | | 0 || |
| + | # [] | ||
|- | |- | ||
| - | |[(1,2 | + | | 1 || |
| + | # [(1,2)] | ||
|- | |- | ||
| - | | | + | | 2 || |
| + | # [(1,2),(1,3)] | ||
| + | # [(1,2),(3,4)] | ||
|- | |- | ||
| - | |[(1,2),(1,3),(1,4),(2,3),(2,4)] | + | | 3 || |
| + | # [(1,2),(1,3),(1,4)] | ||
| + | # [(1,2),(1,3),(2,3)] | ||
| + | # [(1,2),(1,3),(2,4)] | ||
| + | # [(1,2),(1,3),(4,5)] | ||
| + | # [(1,2),(3,4),(5,6)] | ||
|- | |- | ||
| - | |[(1,2),(1,3),(1,4),(2,3),(2,5)] | + | | 4 || |
| + | # [(1,2),(1,3),(1,4),(1,5)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3)] | ||
| + | # [(1,2),(1,3),(1,4),(2,5)] | ||
| + | # [(1,2),(1,3),(1,4),(5,6)] | ||
| + | # [(1,2),(1,3),(2,3),(4,5)] | ||
| + | # [(1,2),(1,3),(2,4),(3,4)] | ||
| + | # [(1,2),(1,3),(2,4),(3,5)] | ||
| + | # [(1,2),(1,3),(2,4),(5,6)] | ||
| + | # [(1,2),(1,3),(4,5),(4,6)] | ||
|- | |- | ||
| - | |[(1,2),(1,3),(1,4),(2,3),(4,5)] | + | | 5 || |
| + | # [(1,2),(1,3),(1,4),(1,5),(1,6)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,4)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,5)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(4,5)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(5,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,5),(2,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,5),(3,5)] | ||
| + | # [(1,2),(1,3),(1,4),(2,5),(3,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,5),(5,6)] | ||
| + | # [(1,2),(1,3),(2,3),(4,5),(4,6)] | ||
| + | # [(1,2),(1,3),(2,4),(3,4),(5,6)] | ||
| + | # [(1,2),(1,3),(2,4),(3,5),(4,5)] | ||
| + | # [(1,2),(1,3),(2,4),(3,5),(4,6)] | ||
|- | |- | ||
| - | |[(1,2),(1,3),(1,4),(2,5),(3,5)] | + | | 6 || |
| + | # [(1,2),(1,3),(1,4),(1,5),(1,6),(2,3)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3),(2,4)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3),(2,6)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3),(4,5)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3),(4,6)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,6),(3,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,4),(3,5)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,4),(5,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,5),(3,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,5),(4,5)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,5),(4,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(4,5),(4,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(4,5),(5,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,5),(2,6),(3,5)] | ||
| + | # [(1,2),(1,3),(1,4),(2,5),(3,5),(4,5)] | ||
| + | # [(1,2),(1,3),(1,4),(2,5),(3,5),(4,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,5),(3,5),(5,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,5),(3,6),(5,6)] | ||
| + | # [(1,2),(1,3),(2,3),(4,5),(4,6),(5,6)] | ||
| + | # [(1,2),(1,3),(2,4),(3,5),(4,6),(5,6)] | ||
|- | |- | ||
| - | |[(1,2),(1,3),(2,4),(3,5),(4,5)] | + | | 7 || |
| + | # [(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(4,5)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,6)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(3,4)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(3,5)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(3,6)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(5,6)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3),(2,6),(3,6)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3),(2,6),(4,5)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3),(2,6),(4,6)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,3),(4,6),(5,6)] | ||
| + | # [(1,2),(1,3),(1,4),(1,5),(2,6),(3,6),(4,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),(5,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,4),(3,5),(4,5)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,4),(3,5),(4,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,4),(3,5),(5,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,5),(3,6),(4,5)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,5),(4,5),(4,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(2,5),(4,6),(5,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,3),(4,5),(4,6),(5,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,5),(2,6),(3,5),(3,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,5),(2,6),(3,5),(4,6)] | ||
| + | # [(1,2),(1,3),(1,4),(2,5),(3,5),(4,6),(5,6)] | ||
|- | |- | ||
| - | | | + | | 8 || par complément de 7 |
|- | |- | ||
| - | | | + | | 9 || par complément de 6 |
|- | |- | ||
| - | | | + | | 10 || par complément de 5 |
|- | |- | ||
| - | | | + | | 11 || par complément de 4 |
|- | |- | ||
| - | | | + | | 12 || par complément de 3 |
| + | |- | ||
| + | | 13 || par complément de 2 | ||
| + | |- | ||
| + | | 14 || par complément de 1 | ||
| + | |- | ||
| + | | 15 || par complément de 0 | ||
| + | |} | ||
| + | || | ||
| + | [[Image:Graphes6.jpg|thumb|200px|Graphes réduits pour n=6]] | ||
|} | |} | ||
== Conclusions == | == Conclusions == | ||
| + | * La vérification du nombre de Ramsey ''R(3,3) = 6'' prend environ 4 minutes (la première fois). | ||
| + | * La lecture des arrêtes des graphes réduits est possible, l'équivalent graphique est plus facile à lire. | ||
| + | * L'affichage des graphes réduits pour ''n = 6'' et un nombre d'arrêtes supérieur à 6 est difficile à lire; l'équivalent graphique est plus facile à lire. | ||
| + | * Il faudrait pouvoir sauvegarder les résultats des graphes réduits sous forme d'un texte, dans un mémo par exemple. | ||
| + | |||
== Ressources == | == Ressources == | ||
* Description de l'algorithme permettant de générer l'ensemble des permutations pour ''n'' donné : [http://web.ew.usna.edu/~wdj/book/node156.html 'An algorithm to list all the permutations'] | * Description de l'algorithme permettant de générer l'ensemble des permutations pour ''n'' donné : [http://web.ew.usna.edu/~wdj/book/node156.html 'An algorithm to list all the permutations'] | ||
* Nombres de Ramsey : [http://mathworld.wolfram.com/RamseyNumber.html 'Ramsey Number'] | * Nombres de Ramsey : [http://mathworld.wolfram.com/RamseyNumber.html 'Ramsey Number'] | ||
* Anecdote sur les nombres de Ramsey : [http://www.grupthink.com/answer/index.php5?id=9528&pap=1 'The Ramsey Number R(3,3)'] | * Anecdote sur les nombres de Ramsey : [http://www.grupthink.com/answer/index.php5?id=9528&pap=1 'The Ramsey Number R(3,3)'] | ||
| + | * Clique maximum ''Using Constraint Programming to Solve the Maximum Clique Problem'' [[Media:MaxcliqueCP03.pdf]] | ||
* Graphes et premier nombre de Ramsey [[Media:Permut_pas.PDB]] | * Graphes et premier nombre de Ramsey [[Media:Permut_pas.PDB]] | ||
* Source [[Permut.pas]] | * Source [[Permut.pas]] | ||
Version actuelle
Sommaire |
Graphes et premier nombre de Ramsey
But
Déterminer les graphes équivalents ayant au plus 6 sommets et utiliser ces graphes pour vérifier le premier nombre de Ramsey R(3,3).
Introduction
Un graphe est constitué d'un nombre n de sommets parfois reliés entre eux par des arrêtes.
Deux graphes sont considérés ici comme équivalents si :
- une permutation des sommets d'un graphe équivaut à l'autre
- pour un graphe chaque arrête est éliminée et chaque absence d'arrête est remplacée par une arrête et qu'il existe une permutation des sommets du graphe qui équivaut à l'autre
Nombre de Ramsey
Le nombre de Ramsey R(n,k) est le nombre minimum de sommets nécessaires pour qu'un graphe contenant un nombre arbitraire d'arrêtes comporte soit n sommets tous reliés entre eux soit k sommets tous non reliés entre eux.
Une autre formulation est le nombre R(n,k) de personnes qu'il faut inviter pour que n personnes se connaissent toutes entre elles ou que k personnes ne se connaissent pas entre elles.
Certains nombres de Ramsey sont connus, entre autres (voir Ressources :
| n | k | R(n,k) |
|---|---|---|
| 3 | 3 | 6 |
| 3 | 4 | 9 |
| 4 | 4 | 18 |
| 5 | 5 | entre 43 et 49 |
| 6 | 6 | entre 102 et 165 |
Anecdote sur les nombres de Ramsey
Paul Erdos disait : "Imaginez une force extraterrestre, vigoureuse et plus puissante que nous qui atterrit et demande la valeur de R(5, 5) où sinon ils détruiront notre planète. Dans ce cas, nous devrions regrouper l'ensemble des ordinateurs et tous nos mathématiciens pour trouver la valeur. Mais supposons, par contre, qu'ils demandent la valeur R(6, 6), nous devrions alors tenter de détruire les extraterrestres." (voir Ressources 'The Ramsey Number R(3,3)')
Permutations
Pour déterminer l'équivalence d'un graphe de n sommets, il faut disposer de la liste complète des permutations pour n éléments donnés.
L'algorithme utilisé est celui décrit dans les ressources.
Il consiste à partir de toutes les permutations de n = 2,
| 1 | 2 |
| 2 | 1 |
de déterminer toutes les permutations pour n = 3 en triplant chaque ligne du cas n = 2
| 1 | 2 |
| 1 | 2 |
| 1 | 2 |
| 2 | 1 |
| 2 | 1 |
| 2 | 1 |
et en insérant le chiffre 3 dans chaque ligne en commençant par la dernière position jusqu'à la première et une fois la première position atteinte, recommencer depuis la première jusqu'à la dernière :
| 1 | 2 | 3 |
| 1 | 3 | 2 |
| 3 | 1 | 2 |
| 3 | 2 | 1 |
| 2 | 3 | 1 |
| 2 | 1 | 3 |
Pour n = 4 il faut quadrupler chaque ligne du cas n = 3 et insérer le chiffre 4 de la même manière que précédemment :
| 1 | 2 | 3 |
| 1 | 2 | 3 |
| 1 | 2 | 3 |
| 1 | 2 | 3 |
| 1 | 3 | 2 |
| 1 | 3 | 2 |
| 1 | 3 | 2 |
| 1 | 3 | 2 |
| 3 | 1 | 2 |
| 3 | 1 | 2 |
| 3 | 1 | 2 |
| 3 | 1 | 2 |
| 3 | 2 | 1 |
| 3 | 2 | 1 |
| 3 | 2 | 1 |
| 3 | 2 | 1 |
| 2 | 3 | 1 |
| 2 | 3 | 1 |
| 2 | 3 | 1 |
| 2 | 3 | 1 |
| 2 | 1 | 3 |
| 2 | 1 | 3 |
| 2 | 1 | 3 |
| 2 | 1 | 3 |
en insérant le chiffre 4 :
| 1 | 2 | 3 | 4 |
| 1 | 2 | 4 | 3 |
| 1 | 4 | 2 | 3 |
| 4 | 1 | 2 | 3 |
| 4 | 1 | 3 | 2 |
| 1 | 4 | 3 | 2 |
| 1 | 3 | 4 | 2 |
| 1 | 3 | 2 | 4 |
| 3 | 1 | 2 | 4 |
| 3 | 1 | 4 | 2 |
| 3 | 4 | 1 | 2 |
| 4 | 3 | 1 | 2 |
| 4 | 3 | 2 | 1 |
| 3 | 4 | 2 | 1 |
| 3 | 2 | 4 | 1 |
| 3 | 2 | 1 | 4 |
| 2 | 3 | 1 | 4 |
| 2 | 3 | 4 | 1 |
| 2 | 4 | 3 | 1 |
| 4 | 2 | 3 | 1 |
| 4 | 2 | 1 | 3 |
| 2 | 4 | 1 | 3 |
| 2 | 1 | 4 | 3 |
| 2 | 1 | 3 | 4 |
Cliques
Un graphe dont tous les sommets sont reliés entre eux s'appelle une clique.
La détermination de la clique maximale d'un graphe s'inspire de l'algorithme décrit dans les ressources (Using Constraint Programming to Solve the Maximum Clique Problem).
Le principe de l'algorithme se base sur le fait que dans une clique d'ordre n, si un sommet et ses arrêtes qui le reliait aux autres sont supprimés, alors le graphe est une clique d'ordre n - 1.
La fonction omega implémente cette détermination, associée à la fonction gamma qui détermine les nœuds associés à un sommet et la fonction limitlinks qui supprime un sommet et les arrêtes associées.
Résultats
Statistiques
| Nœuds | Arrêtes | Graphes | Permutations | Graphes réduits | Durée des calculs en secondes |
|---|---|---|---|---|---|
| 2 | 1 | 2 | 2 | 2 | 0 |
| 3 | 3 | 8 | 6 | 4 | 0 |
| 4 | 6 | 64 | 24 | 11 | 0 |
| 5 | 10 | 1024 | 120 | 34 | 1 |
| 6 | 15 | 32768 | 720 | 156 | 229 |
- Nœuds : n
- Arrêtes : n x (n - 1) / 2
- Graphes : 2 ^ (n x (n - 1) / 2)
- Permutations : n!
- Graphes réduits : graphes équivalents sous les permutations
Graphes réduits pour n = 2
|
Graphes réduits pour n = 3
|
Graphes réduits pour n = 4
|
Graphes réduits pour n = 5
|
Graphes réduits pour n = 6
|
Conclusions
- La vérification du nombre de Ramsey R(3,3) = 6 prend environ 4 minutes (la première fois).
- La lecture des arrêtes des graphes réduits est possible, l'équivalent graphique est plus facile à lire.
- L'affichage des graphes réduits pour n = 6 et un nombre d'arrêtes supérieur à 6 est difficile à lire; l'équivalent graphique est plus facile à lire.
- Il faudrait pouvoir sauvegarder les résultats des graphes réduits sous forme d'un texte, dans un mémo par exemple.
Ressources
- Description de l'algorithme permettant de générer l'ensemble des permutations pour n donné : 'An algorithm to list all the permutations'
- Nombres de Ramsey : 'Ramsey Number'
- Anecdote sur les nombres de Ramsey : 'The Ramsey Number R(3,3)'
- Clique maximum Using Constraint Programming to Solve the Maximum Clique Problem Media:MaxcliqueCP03.pdf
- Graphes et premier nombre de Ramsey Media:Permut_pas.PDB
- Source Permut.pas
Catégories: Logiciel | Pascal | Palm